GJK算法

发表于 分类于 ，

这篇文章是对于GAMES 104游戏引擎物理系统一节中GJK算法的学习总结。

Minkowski Sum 闵可夫斯基和

首先明确，一个闭合形状可以通过边界点集来定义。

对于两个形状 $A$ 和 $B$ 来说，他们的闵可夫斯基和即为两个集合中的点两两相加形成的点集，记作 $A+B$ 。一个直观的理解就是将其中的一个形状 $A$ 所在坐标系的原点平移到另一个形状 $B$ 的边界上，并沿着 $B$ 的边界扫过一周，这样得到的新边界即为Minkowski Sum，如下图所示：

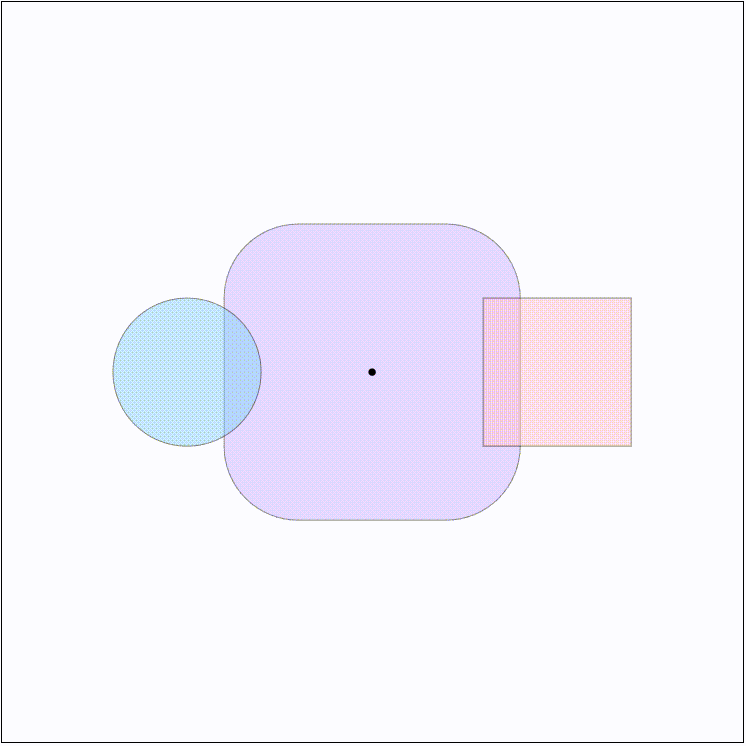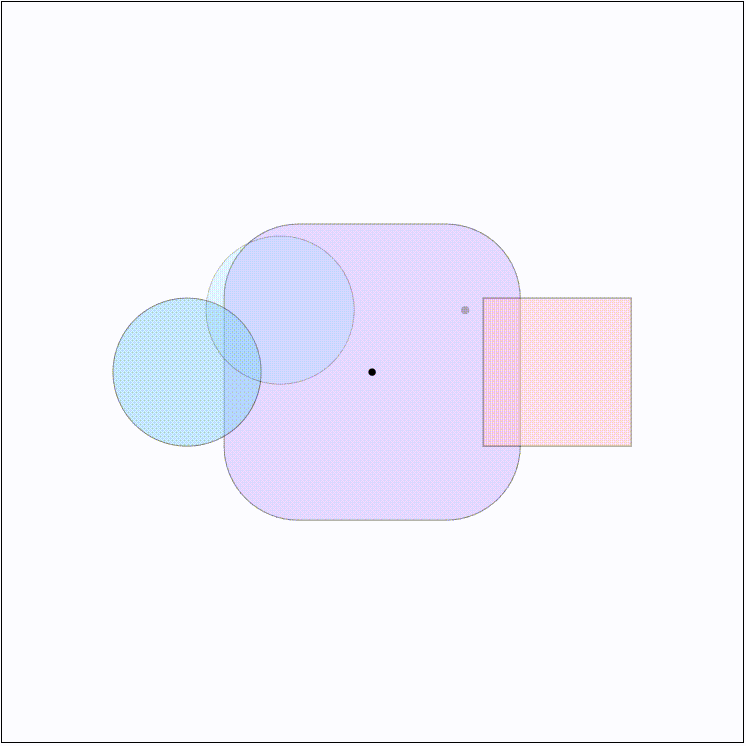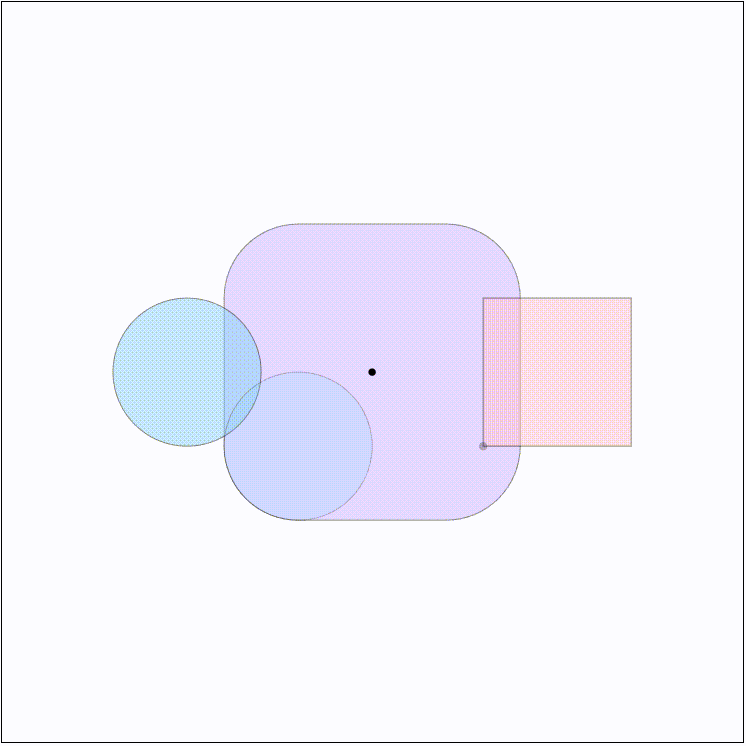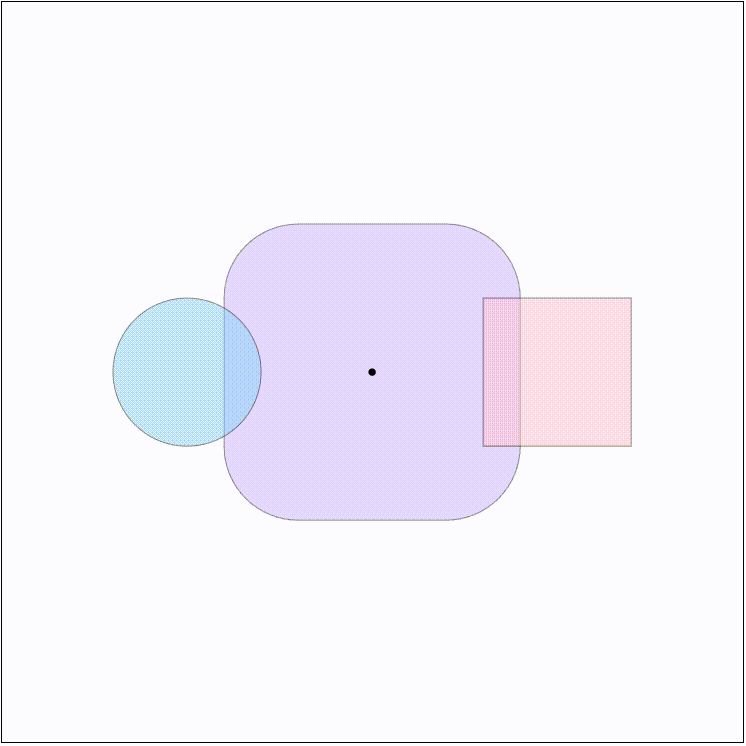
intuition

闵可夫斯基和有一个重要的性质，即闵可夫斯基和的凸包等于两个形状各自凸包的闵可夫斯基和。这样的话，如果两个形状本就是凸的话，Minkowski Sum的凸包就会恰好包含两个形状内无穷多个点两两相加的结果。

Minkowski Difference 闵可夫斯基差

如果两个形状相交的话，那么一定会存在至少一对 $A$ 和 $B$ 中的点 $p_A$ 和 $p_B$ ，使得 $p_A-p_B=0$ 。尝试将这个观察与上面所述的Minkowski Sum联系起来，定义闵可夫斯基差为 $A-B=A+(-B)$ ， $(-B)$ 即 $B$ 中的点绕原点翻转后得到的点集。

P.S. 按照Wiki上的说法，这其实不是Minkowski Difference的正统定义，而是Hermann Minkowski，不过在碰撞检测中只会用到上面的定义，这里就不再深究区别了。

根据Minkowski Sum的性质， $A-B$ 的中含中包含了所有点对的差值。也就是说如果这个凸包能够包围原点的话，这两个形状就是相交的。这样我们就把一个本来要做无穷次判断才能得到答案的问题成功转化为了一个有界的问题。乍一看，单纯按照这种方法来测试的话复杂度仍是平方级别的。可以证明得到的凸包至多只有 $|A|+|B|$ 个顶点，[3]中给出了在 $O(n\log n)$ 内直接构造Minkowski Sum凸包的算法，大致的思路就是首先按照逆时针的顺序对于两个点集中的顶点排序，再使用双指针比较Polar Angle来保证不重不漏，具体可以参考原文章，这里我们不会用到这种算法。

GJK算法

当两个形状的点数很多时，由于我们的目标只是判断包不包含原点，相应闵可夫斯基差的凸包可能会有很多冗余。比如在2D的情况下，我们实际上只需要判断闵可夫斯基差中最接近原点的三个点与原点的关系即可。这就是GJK算法的Motivation。

单纯形定义为 n 维空间中最简单的几何体，比如在2D空间中就是三角形，3D空间中就是四面体。GJK 是一个迭代算法。它的目标是构建一个位于 $A-B$ 内部的单纯形，并检查这个单纯形是否包含原点。

GJK算法引入了支撑函数的概念，用于感知形状的边界。支撑函数的定义如下：给定一个方向向量 $d$，形状 $C$ 的支撑函数返回在 $C$ 中沿着方向 $d$ 最远的点。支撑函数的一个关键特性是：闵可夫斯基差的支撑点可以通过原形状 $A$ 和 $B$ 的支撑点来计算，即support(A - B, d) = support(A, d) - support(B, -d)，这点也很直观。

GJK的伪代码如下。NearestSimplex(s)会接收一个若干维单纯形 $s$ ，返回 $s$ 上离原点最近的子部分（比如对于三角形可能返回的是一个三角形或是低一维即一维单纯形的线段）、从简化后的单纯形指向原点最近的方向向量（比如简化后的单纯形是线段时返回线段的垂足到原点的方向向量）以及判断原点是否在单纯形内的判断结果。

1
2
3
4
5
6
7
8
9
10
11
12
13
function GJK_intersection(shape p, shape q, vector initial_axis):
    vector  A = Support(p, initial_axis) − Support(q, −initial_axis)
    simplex s = {A}
    vector  D = −A

    loop:
        A = Support(p, D) − Support(q, −D)
        if dot(A, D) < 0:
            reject
        s = s ∪ {A}
        s, D, contains_origin := NearestSimplex(s)
        if contains_origin:
            accept

对于GJK算法的说明如下：

  • dot(A, D) < 0说明支撑点在接近原点的方向向量的投影比原点要近，由于支撑点已经是最接近原点的点了，因此这个代表闵可夫斯基差的单纯形就绝不可能包含原点了，可以直接返回reject。
  • NearestSimplex(s)内对于单纯形的处理如下，以输入为三角形 $ABC$ 为例，步骤如下：
    • 检查原点 $O$ 是否在 $AB$ 的内侧，可通过计算 (B - A) × (O - A) 的符号来判断。如果 $ABC$ 逆时针排列则叉积的结果小于$0$则在外侧，否则为内侧。
    • 同样地，检查边 $BC$ 和 $CA$。
    • 若是都在内侧，直接返回。
    • 否则原点一旦在任意一条边的外侧，则将单纯形简化为这条边对应的线段（即更靠近原点的子部分），同时返回从该线段指向原点的垂直方向。

总的来说，GJK通过迭代维护了闵可夫斯基差的一个最接近原点的子集，利用这个子集作为闵可夫斯基差的代理来判断是否包含原点，从而大大提高了算法的效率。

具体的实现先挖个坑 ;)

EPA算法 (Expanding Polytope Algorithm)

EPA算法算是GJK的扩展，当检测到碰撞时，EPA可以算出来穿透方向和穿透深度，当我们需要把两个物体分离时会很有用。这部分也暂时留个坑，可以先参考[4]。

参考

  1. GJK算法的Wiki
  2. GJK算法的可视化展示
  3. Minkowski sum of convex polygons
  4. EPA (Expanding Polytope Algorithm)