PBR探微:Disney BSDF
\[ \newcommand{\d}{\mathrm{d}} \newcommand{\norm}[1]{\left\| #1 \right\|} \]
前言
最近突然又想去搓一个离线渲染器作为玩具项目了,趁机深入看了下Disney Principled BSDF,也算是又从头学了一遍PBR,谨将所学的东西略微记下,以便后续查阅。
基本定义
由于Disney BSDF涉及大量的公式,这里有必要重新对于所有的公式和定义进行澄清。
NDF
法线分布函数NDF究竟是什么?之前我的视线总是聚焦于具体的公式如Beckmann,GGX和GTR等等,很少会去关注NDF的定义。其实在不久之前,我还以为NDF就是法线分布的pdf,满足半球面上的积分为一即可,然而NDF的定义却并非如此。
[1]中对于NDF的描述是
the statistical distribution of surface normals m over the microsurface,这里的\(\mathrm{m}\)指的就是微观法线,也就是我们常说的半程向量\(\mathrm{h}\)。乍一看这个定义似乎说的还是pdf,但NDF实际上是用微观面积与宏观面积的比值来定义的。具体来说,定义宏观面积的微元为\(\mathrm{d}A\),微观法线\(\mathrm{m}\)对应的立体角微元为\(\mathrm{d}\mathrm{\omega}_m\),那么\(D(\mathrm{m})\mathrm{d}\mathrm{\omega}_m\mathrm{d}A\)就等于(微观)法线朝向为\(\mathrm{m}\)微平面的总面积,因此\(D(\mathrm{m})\)项可以写为,其中\(\mathrm{d}A_m\)代表微平面的面积:
\[D(\mathrm{m})=\frac{\d A_m}{\d \mathrm{\omega}_m\mathrm{d}A}\]
然后来看下\(D\)的归一化条件,首先易得微平面投影面积的积分应该为\(\mathrm{d}A\):
\[\mathrm{d}A=\int(n \cdot m)\mathrm{d}A_m\]
将\(D(\mathrm{m})\)的定义带入后可得真正的归一化条件:
\[\int_{\Omega}(n \cdot m)D(\mathrm{m})\mathrm{d}\mathrm{\omega}_m=1\]
之后就不要再天真地把\(D(\mathrm{m})\)项看作pdf了,而将其称为面积密度则更合适。
P.S. [1]中Walter et al. 实际上给出了更严格的归一化条件,即对于任意的方向\(\mathrm{v}\)需要满足:
\[\int_{\Omega}(v \cdot m)D(\mathrm{m})\mathrm{d}\mathrm{\omega}_m=(v \cdot m)\]
Shadowing-Masking Function G
\(G\)项是为了能量守恒而加上的,用于描述有多少的微平面是在入射方向\(\mathrm{}\)\(\mathrm{i}\)和出射方向\(\mathrm{}\)\(\mathrm{o}\)上都是可见的,\(G\)要满足的三个条件分别是:
- 位于0-1之间,这个没啥问题
- 可逆性reciprocity, 交换\(\mathrm{i}\)和\(\mathrm{o}\)不影响\(G\)的值
- 微平面始终只有一侧是可见的,即当\((\mathrm{i} \cdot \mathrm{n})(\mathrm{i} \cdot \mathrm{m}) \le 0\)(\(\mathrm{o}\)同理)时\(G\)为0
由于\(G\)项依赖于微表面的细节,因此一般情况下不存在解析解,现有的模型如Smith包含了大量的统计近似和几何简化,这里就不再赘述。
Smith中为了满足可逆性,特意将\(G\)项设计为了可分离的形式(这似乎是个很通用的技巧,Kulla-Conty Approximation也是这么干的),即\(G(\mathrm{i},\mathrm{o},\mathrm{m})=G_1(\mathrm{i},\mathrm{m})G_1(\mathrm{o},\mathrm{m})\)。
微平面BSDF模型
既然已经准备深入PBR了,那微平面模型的推导肯定少不了,紧跟[1]的思路,可以得到一看看起来非常吓人的宏观表面BSDF积分定义,注意不是渲染方程的那个积分!
\[ f_s(\mathrm{i},\mathrm{o},\mathrm{m})=\displaystyle \int \left| \dfrac{\mathrm{i} \cdot \mathrm{m}}{\mathrm{i} \cdot \mathrm{n}} \right| f_s^m(\mathrm{i},\mathrm{o},\mathrm{m}) \left| \dfrac{\mathrm{o} \cdot \mathrm{m}}{\mathrm{o} \cdot \mathrm{n}} \right| G(\mathrm{i},\mathrm{o},\mathrm{m}) D(\mathrm{m}) \d\mathrm{\omega}_m \label{eq:1} \tag{1} \]
其中\(f_s^m(\mathrm{i},\mathrm{o},\mathrm{m})\)为微平面本身的BSDF,虽然常用的模型都假设了微表面为镜面,但是这里暂时先只列出一般形式,这也是不把\(\mathrm{m}\)直接写作\(\mathrm{h}\)的原因。
为了搞懂这个式子,先关注后面的部分,\(G\)和\(D\)的乘积代表了微观法线朝向为\(\mathrm{m}\)的微平面面积之和占宏观面积的比例,这点很好理解。
最神秘的是那两个点积构成的系数,它们实则充当了宏观与微观间的桥梁,按照论文的意思就是,第一个系数会把incident irradiance从macro尺度转换到micro,第二个系数会把radiance转换回macro尺度。尝试着来理解下为什么要用到这两个系数。
第一个系数
宏观表面是与入射方向\(\mathrm{i}\)是成角度的,除以\((\mathrm{i} \cdot \mathrm{n})\),是为了抵消这个角度带来的衰减,还原真正的incident irradiance,也就是垂直辐照度。微观表面的法线也与入射方向\(\mathrm{i}\)有角度,既然有了真正的incident irradiance,那么只需要再乘上\((\mathrm{i} \cdot \mathrm{m})\)就能得到微表面接收到的irradiance了。这两步合起来就是第一个系数了。
第二个系数
经过实际微表面的反射后就是出射的radiance了,不妨以radiant exitance(也就是出射的irradiance)作为桥梁把radiance从微观尺度转换为宏观尺度的数值。从radiance的定义出发,只要乘上\(\mathrm{d}\mathrm{\omega}_o(\mathrm{o} \cdot \mathrm{m})\)就能得到radiant exitance了;同样,radiant exitance除以\(\mathrm{d}\mathrm{\omega}_o(\mathrm{o} \cdot \mathrm{n})\)就是宏观的radiance了。这样我们就得到了第二个系数。
微表面的BSDF(BRDF+BSDF)
虽说上面是一般的式子,但是为了方便,大多数模型都会假定微平面是完全光滑的,只遵从Fresnel和Snell定律进行反射和折射。设\(\rho(\mathrm{i},\mathrm{m})\)代表散射的比例,\(\mathrm{s}(\mathrm{i},\mathrm{m})\)为理论上应该散射的方向,那么镜面的BSDF可以定义为: \[ f_s^m(\mathrm{i},\mathrm{o},\mathrm{m})=\rho\dfrac{\delta_{\omega_o}(\mathrm{s},\mathrm{o})}{\left| \mathrm{o} \cdot \mathrm{m} \right|} \tag{2} \] 上式中\(\delta_{\omega_o}(\mathrm{s},\mathrm{o})\)为仅在\(\mathrm{s}\)处有值的Dirac函数,分布上的点积是为了保证能量守恒而加上的。接下来就是考虑如何把这个式子应用到(1)中。
既然已经假定微表面是镜面了,半程向量\(\mathrm{h}(\mathrm{i},\mathrm{o})\)的概念也就可用了,用\(\mathrm{h}\)替代\(\mathrm{s}\)并带入到(2)中可得(3)。注意这里乘上Jacobian,是因为Dirac本身只有在积分时才是有意义的,(2)式只能算是一个简单写法;\(\mathrm{s}\)又与积分变量\(\mathrm{o}\)相关,所以在进行代换时需要乘上Jacobian才能保持积分值不变。 \[ f_s^m(\mathrm{i},\mathrm{o},\mathrm{m})=\rho(\mathrm{i},\mathrm{m})\dfrac{\delta_{\omega_o}(\mathrm{h}(\mathrm{i},\mathrm{o}),\mathrm{m})}{\left| \mathrm{o} \cdot \mathrm{m} \right|} \norm{\dfrac{\partial\mathrm{\omega}_h}{\partial\mathrm{\omega}_o}} \tag{3} \]
Reflection BRDF
[1]和[3]中分别给出了Jacobian的计算方法,个人认为[3]中的比较清晰,在此复述一遍。下面的示意图来自[3],注意图中的\(\mathrm{o}\)和\(\mathrm{i}\)和我们讨论中的定义相反,\(\mathrm{m}\)就是半程向量。下面会先按照图中给出的符号进行推导,最后再替换为我们的符号。
从几何关系中可以很容易看出固定\(\mathrm{o}\)时并移动\(\mathrm{m}\)时,\(\d \theta_i=2\d \theta_m\),然后是比较有意思的一步,直接以\(\mathrm{o}\)而非\(\mathrm{m}\)作为up vector来建立球面坐标系,这样子\(\theta_i\)和\(\theta_m\)就成\(\mathrm{i}\)和\(\mathrm{m}\)与\(\mathrm{o}\)的夹角了,另外在retro reflection的情况下还能得到\(\theta_i=\theta_m=0\),然后很容易就能看出(解一个微分方程)\(\theta_i=2\theta_m\),将立体角表示为球坐标后开始计算Jacobian:
\[ \begin{aligned} \dfrac{\d\mathrm{\omega}_h}{\d\mathrm{\omega}_i} &= \dfrac{\sin \theta_m \d \theta_m \d \phi_m}{\sin \theta_i \d \theta_i \d \phi_i} \\ &= \dfrac{\sin \theta_m \d \theta_m \d \phi_m}{\sin 2\theta_m (2\d \theta_m) \d \phi_m} \\ &= \dfrac{\sin \theta_m}{4\sin \theta_m \cos \theta_m } \\ &= \dfrac{1}{4\cos \theta_m } \\ &= \dfrac{1}{4(\mathrm{i} \cdot \mathrm{m})} = \dfrac{1}{4(\mathrm{o} \cdot \mathrm{m})} \end{aligned} \] 来计算微表面的反射部分,直接把菲涅尔项和Jacobian带进去即可。注意\((\mathrm{i} \cdot \mathrm{h}_r)=(\mathrm{o} \cdot \mathrm{h}_r)\)。 \[ f_r^m(\mathrm{i},\mathrm{o},\mathrm{m})=F(\mathrm{i},\mathrm{m})\dfrac{\delta_{\omega_o}(\mathrm{h}_r,\mathrm{m})}{4(\mathrm{i} \cdot \mathrm{h}_r)^2} \tag{4} \]
Refraction(Transmission) BRDF
虽然[1]对于这部分的推导使用了折射半程向量\(\mathrm{h}_t\)的概念,但这里的\(\mathrm{h}_t\)实际上指的就是微平面的法线。这里还要做一些补充,笔者也是在写的时候才意识到,就是微平面\(\mathrm{m}\)实际上只是一个统计和建模上的概念,因为一个无限小平面的朝向是不可知的。唯一能做的就是从镜面的假设出发,通过实际观测到的\(\mathrm{i}\)和\(\mathrm{o}\)来算一个半程向量\(\mathrm{h}\),并通过Dirac函数来筛选出朝向正好为\(\mathrm{h}\)的平面。因此,\(\mathrm{h}_r\)、\(\mathrm{h}_t\)和\(\mathrm{m}\)在实际计算时都是同一个向量,在折射的情况下称其为”半程向量”实际上是不名副其实的,不过为了推导上的统一我们就不再引入新的符号了。
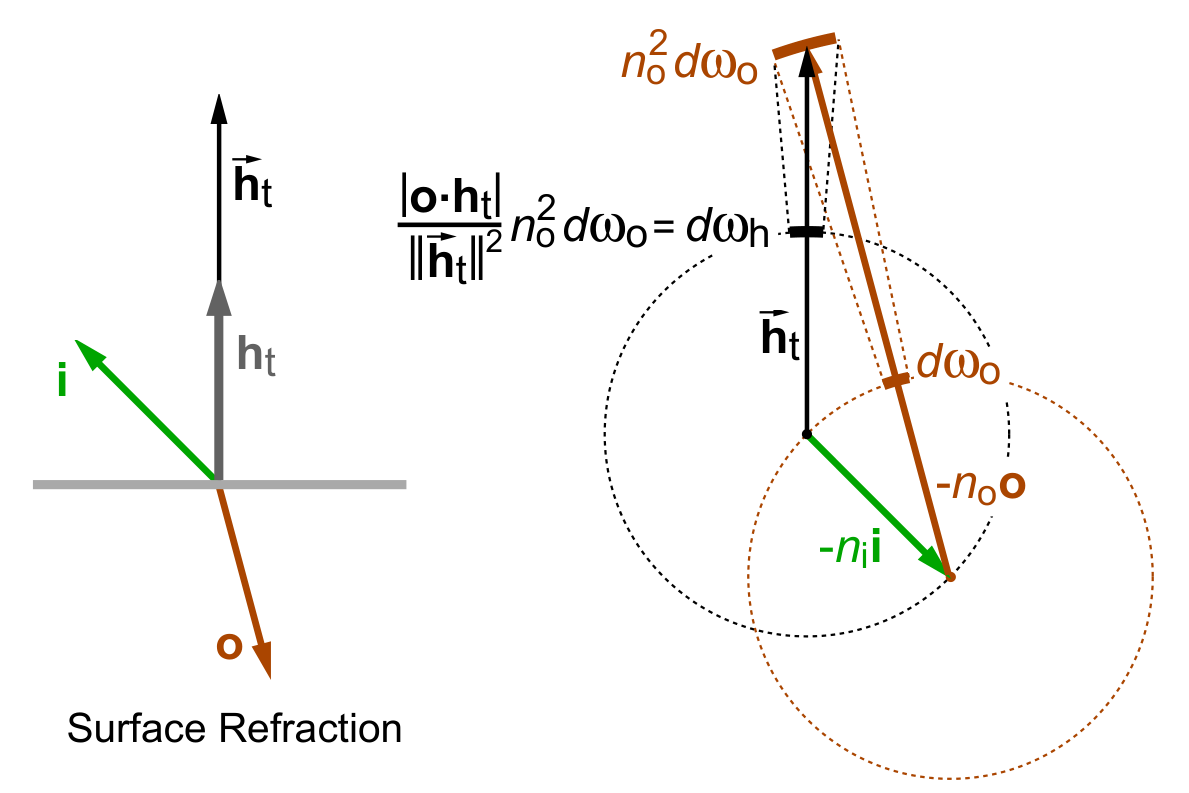
如何计算微观法线呢?首先从上图的左边可以观察到\(\mathrm{i}\)和\(\mathrm{o}\)垂直于\(\mathrm{h}_t\)分量的模长分别为对应折射角的正弦值,同时分量的方向相反。根据斯涅尔定律\(\eta_i\sin\theta_i=\eta_o\sin\theta_o\),两者相加正好完全抵消,剩下的部分正好是与微观法线共线的,做一次归一化就行了。记归一化与未归一化的半程向量分别为\(\mathrm{h}_t\)和\(\vec{\mathrm{h}}_t\),则 \[ \vec{\mathrm{h}}_t=-(\eta_i\mathrm{i}+\eta_o\mathrm{o}), \mathrm{h}_t(\mathrm{i},\mathrm{o})=\frac{\vec{\mathrm{h}}_t}{\Vert \vec{\mathrm{h}}_t \Vert} \tag{5} \] 至于Jacobian,[1]给出了几何的解释,如上图的右半部分。Gemini也给出了一个大概的推导,为了转换为立体角之间的关系,需要得到\(\vec{\mathrm{h}}_t\)和\(\mathrm{o}\)变化时微分面积的对应关系。首先在(5)式\(\vec{\mathrm{h}}_t\)的两端求导,得到\(\d \vec{\mathrm{h}}_t=\eta_o \d \mathrm{o}\),这说明当\(\mathrm{o}\)变化时\(\vec{\mathrm{h}}_t\)扫过的微分面积是\(\mathrm{o}\)扫过面积的\(\eta_o^2\)倍。但这个面积是垂直与\(\mathrm{o}\)的,还要投影到垂直于\(\vec{\mathrm{h}}_t\)的方向上,因此还要乘上\(\left| \mathrm{o} \cdot \vec{\mathrm{h}}_t \right|\)才是真正的微分面积。根据立体角的定义,还要除以半径的平方,而\(\norm{\vec{\mathrm{h}}_t}=\mathrm{h}_t \cdot \vec{\mathrm{h}}_t\),最终可以得到Jacobian为: \[ f_t^m(\mathrm{i},\mathrm{o},\mathrm{m})=(1-F(\mathrm{i},\mathrm{m}))\dfrac{\delta_{\omega_o}(\mathrm{h}_t,\mathrm{m}) \eta_o^2}{(\eta_i(\mathrm{i} \cdot \mathrm{h}_t)+\eta_o(\mathrm{o} \cdot \mathrm{h}_t))^2} \tag{6} \] [4]中的一段也与这段推导相呼应:
1 | Snell’s law describes the bending of rays, but less obviously, it also describes the spreading of rays. Specifically, the apparent radiance of a refracted ray will be scaled by η2 which, as Veach shows [Vea97], is equivalent to the change in projected solid angle. |
当然,从上面的式子我们也能看出BTDF是不满足可逆性的,因为Radiance被缩放了\(\eta^2\)倍,双向的BTDF关系如下: \[ \dfrac{f_t^m(\mathrm{i},\mathrm{o},\mathrm{m})}{\eta_o^2}=\dfrac{f_t^m(\mathrm{o},\mathrm{i},\mathrm{m})}{\eta_i^2} \]
BSDF
有了(1)、(4)和(6)式,我们终于能写出最终的BSDF了,由于Dirac函数的存在,宏观表面的BSDF可以看作是反射和折射两部分的叠加: \[ f_s(\mathrm{i},\mathrm{o},\mathrm{n})=f_r(\mathrm{i},\mathrm{o},\mathrm{n})+f_t(\mathrm{i},\mathrm{o},\mathrm{n}) \tag{7} \] 经过消元,反射部分为,就是我们熟悉的Cook-Torrance BRDF: \[ f_r(\mathrm{i},\mathrm{o},\mathrm{n})=\dfrac{F(\mathrm{i},\mathrm{h}_r)G(\mathrm{i},\mathrm{o},\mathrm{h}_r)D(\mathrm{h}_r)}{4 \left| \mathrm{i} \cdot \mathrm{n} \right| \left| \mathrm{o} \cdot \mathrm{n} \right|} \]
折射部分基本上没什么可消元的,就是单纯把微平面的\(f_t^m\)带进去即可: \[ f_t(\mathrm{i},\mathrm{o},\mathrm{n})=\left| \dfrac{\mathrm{i} \cdot \mathrm{h}_t}{\mathrm{i} \cdot \mathrm{n}} \right| \left| \dfrac{\mathrm{i} \cdot \mathrm{h}_t}{\mathrm{o} \cdot \mathrm{n}} \right| \dfrac{\eta_o^2(1-F(\mathrm{i},\mathrm{h}_t))G(\mathrm{i},\mathrm{o},\mathrm{h}_t)D(\mathrm{h}_t)}{(\eta_i(\mathrm{i} \cdot \mathrm{h}_t)+\eta_o(\mathrm{o} \cdot \mathrm{h}_t))^2} \]